Question

(Numerical Data Representation) How many bits per word are required to represent the following positive decimal integers: a.0 through 100b.0 through 255c.0 through 256d.0 through 10,000,000

Answer 1

a. 7 bits

b. 8 bits

c. 9 bits

d. 24 bits

Step-by-step explanation:

Required

Number of bits per word

The formula to get the number of bits per word is:

`2^n = N`

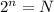
Where

n = bits

N = numbers

Solving (a) 0 to 100

There are 101 digits between 0 and 100 (inclusive)

So:

`N = 101`

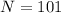
Substitute 101 for N in
`2^n = N`

`2^n = 101`

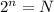
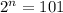
101 can not be expressed as an exponent of 2.

So, we substitute 101 for the closest number greater than 101 that can be expressed as an exponent of 2.

So:

`2^n = 128`

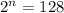
Express 128 as an exponent of 2

`2^n = 2^7`

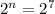
Apply law of indices

`n = 7`

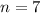
Hence, 7 bits are required

Solving (b): 0 through 255

There are 256 digits between 0 and 255 (inclusive)

So:

`N = 256`

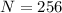
Substitute 256 for N in
`2^n = N`

`2^n = 256`

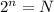
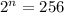
Express 256 as an exponent of 2

`2^n = 2^8`

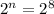
Apply law of indices

`n = 8`

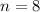
Hence, 8 bits are required

Solving (c): 0 through 256

There are 257 digits between 0 and 256 (inclusive)

So:

`N = 257`

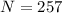
Substitute 257 for N in
`2^n = N`

`2^n = 257`

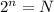
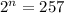
257 can not be expressed as an exponent of 2.

So, we substitute 257 for the closest number greater than 101 that can be expressed as an exponent of 2.

So:

`2^n = 512`

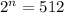
Express 512 as an exponent of 2

`2^n = 2^9`

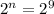
Apply law of indices

`n = 9`

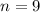
Hence, 9 bits are required

Solving (d): 0 through 10000000

There are 10000001 digits between 0 and 10000000 (inclusive)

So:

`N = 10000000`

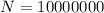
Substitute 10000000 for N in
`2^n = N`

`2^n = 10000000`

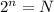
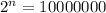
10000000 can not be expressed as an exponent of 2.

So, we substitute 10000000 for the closest number greater than 101 that can be expressed as an exponent of 2.

So:

`2^n = 16777216`

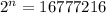
Express 16777216 as an exponent of 2

`2^n = 2^{24`

Apply law of indices

`n = 24`

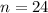
Hence, 24 bits are required