Question

The probability is 1 in 4,011,000 that a single auto trip in the United States will result in a fatality. Over a lifetime, an average U.S. driver takes 46,000 trips.(a) What is the probability of a

Answer 1

0.0114

Explanation:

(a) What is the probability of a fatal accident over a lifetime?

Suppose A be the event of a fatal accident occurring in a single trip.

Given that:

P(1 single auto trip in the United States result in a fatality) = P(A)

Then;

P(A) = 1/4011000

P(A) = 2.493 × 10⁻⁷

Now;

P(1 single auto trip in the United States NOT resulting in a fatality) is:

P(
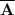`\mathbf{\overline A}`) = 1 - P(A)

P(
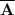`\mathbf{\overline A}`) = 1 - 2.493 × 10⁻⁷

P(
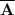`\mathbf{\overline A}`) = 0.9999997507

However, P(fatal accident over a lifetime) = P(at least 1 fatal accident in lifetime i.e. 46000 trips)

= 1 - P(NO fatal accidents in 46000 trips)

Similarly,

P(No fatal accidents over a lifetime) = P(No fatal accident in the 46000 trips) = P(No fatality on the 1st trip and No fatality on the 2nd trip ... and no fatality on the 45999 trip and no fatality on the 46000 trip)

=
`[P(\overline A)] ^(46000) \ \ \ (since \ trips \ are \ independent \ events)`

=
`[0.9999997507]^(46000)`

= 0.9885977032

Finally;

P(fatal accident over a lifetime) = 1 - 0.9885977032

P(fatal accident over a lifetime) = 0.0114022968

P(fatal accident over a lifetime) ≅ 0.0114