Question

4) – 2x2 + 6x + 5 = 0

a. nonreal
b. real, irrational, and unequal
c. real, rational, and equal
d. real, rational, and unequal

Answer 1

b. real, irrational, and unequal

Explanation:

Roots of a quadratic equation

The standard representation of a quadratic equation is:

`ax^2+bx+c=0`

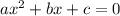
where a,b, and c are constants.

Solving with the quadratic formula:

`\displaystyle x=(-b\pm √(b^2-4ac))/(2a)`

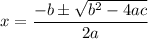
The argument of the radical is called the discriminant:

`d=b^2-4ac`

The nature of the solutions of the equation depends on the value of d as follows:

• If d is zero, there is only one real (and rational) root.
• If d is positive, there are two real unequal roots. If also d is a perfect square, then the roots are also rational. If d is not a perfect square, the roots are irrational.
• If d is negative, there are two unequal complex roots.

We are given the equation:

`-2x^2+6x+5=0`

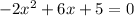
Here: a=-2, b=6, c=5. The discriminant is:

`d=6^2-4(-2)(5)=36+80=116`

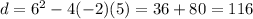
d = 116

Since d is positive and a non-perfect square, the roots are:

b. real, irrational, and unequal