Question

If you are given a3=2 a5=16, find a100.

Answer 1

I suppose
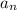`a_n` denotes the n-th term of some sequence, and we're given the 3rd and 5th terms
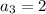`a_3=2` and
`a_5=16`. On this information alone, it's impossible to determine the 100th term
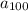`a_(100)` because there are infinitely many sequences where 2 and 16 are the 3rd and 5th terms.

To get around that, I'll offer two plausible solutions based on different assumptions. So bear in mind that this is not a complete answer, and indeed may not even be applicable.

• Assumption 1: the sequence is arithmetic (a.k.a. linear)

In this case, consecutive terms differ by a constant d, or

`a_n = a_(n-1) + d`

By this relation,

`a_(n-1) = a_(n-2) + d`

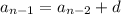
and by substitution,

`a_n = (a_(n-2) + d) + d = a_(n-2) + 2d`

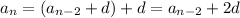
We can continue in this fashion to get

`a_n = a_(n-3) + 3d`

`a_n = a_(n-4) + 4d`

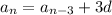
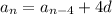
and so on, down to writing the n-th term in terms of the first as

`a_n = a_1 + (n-1)d`

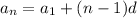
Now, with the given known values, we have

`a_3 = a_1 + 2d = 2`

`a_5 = a_1 + 4d = 16`

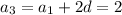
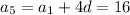
Eliminate
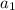`a_1` to solve for d :

`(a_1 + 4d) - (a_1 + 2d) = 16 - 2 \implies 2d = 14 \implies d = 7`

Find the first term
`a_1` :

`a_1 + 2*7 = 2 \implies a_1 = 2 - 14 = -12`

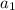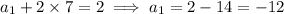
Then the 100th term in the sequence is

`a_(100) = a_1 + 99d = -12 + 99*7 = \boxed{681}`

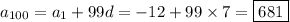
• Assumption 2: the sequence is geometric

In this case, the ratio of consecutive terms is a constant r such that

`a_n = r a_(n-1)`

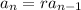
We can solve for
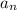`a_n` in terms of
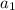`a_1` like we did in the arithmetic case.

`a_(n-1) = ra_(n-2) \implies a_n = r\left(ra_(n-2)\right) = r^2 a_(n-2)`

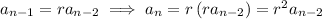
and so on down to

`a_n = r^(n-1) a_1`

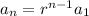
Now,

`a_3 = r^2 a_1 = 2`

`a_5 = r^4 a_1 = 16`

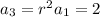
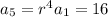
Eliminate
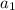`a_1` and solve for r by dividing

`(a_5)/(a_3) = (r^4a_1)/(r^2a_1) = \frac{16}2 \implies r^2 = 8 \implies r = 2\sqrt2`

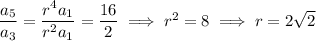
Solve for
`a_1` :

`r^2 a_1 = 8a_1 = 2 \implies a_1 = \frac14`

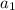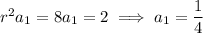
Then the 100th term is

`a_(100) = \frac{(2\sqrt2)^(99)}4 = \boxed{\frac{\sqrt{8^(99)}}4}`

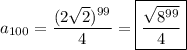
The arithmetic case seems more likely since the final answer is a simple integer, but that's just my opinion...