I suppose
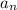 denotes the n-th term of some sequence, and we're given the 3rd and 5th terms
denotes the n-th term of some sequence, and we're given the 3rd and 5th terms
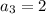 and
and
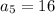 . On this information alone, it's impossible to determine the 100th term
. On this information alone, it's impossible to determine the 100th term
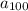 because there are infinitely many sequences where 2 and 16 are the 3rd and 5th terms.
because there are infinitely many sequences where 2 and 16 are the 3rd and 5th terms.
To get around that, I'll offer two plausible solutions based on different assumptions. So bear in mind that this is not a complete answer, and indeed may not even be applicable.
• Assumption 1: the sequence is arithmetic (a.k.a. linear)
In this case, consecutive terms differ by a constant d, or
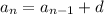
By this relation,
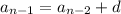
and by substitution,
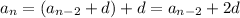
We can continue in this fashion to get
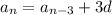
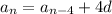
and so on, down to writing the n-th term in terms of the first as
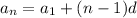
Now, with the given known values, we have
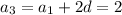
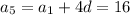
Eliminate
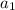 to solve for d :
to solve for d :

Find the first term
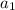 :
:
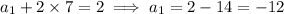
Then the 100th term in the sequence is
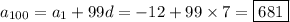
• Assumption 2: the sequence is geometric
In this case, the ratio of consecutive terms is a constant r such that
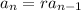
We can solve for
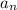 in terms of
in terms of
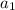 like we did in the arithmetic case.
like we did in the arithmetic case.
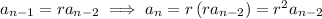
and so on down to
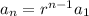
Now,
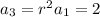
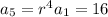
Eliminate
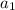 and solve for r by dividing
and solve for r by dividing
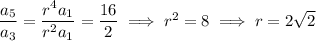
Solve for
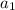 :
:
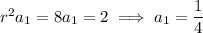
Then the 100th term is
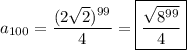
The arithmetic case seems more likely since the final answer is a simple integer, but that's just my opinion...