Question

Prove the trigonometric identity

Answer 1

Proved See below

Explanation:

Man this one is a world of its own :D Just a quick question are you a fellow Add Math student in O levels i remember this question from back in the day :D Anyhow Lets get started

For this question we need to know the following identities:

`1+tan^(2)x=sec^2x\\\\1+cot^2x=cosec^2x\\\\sin^2x+cos^2x=1`

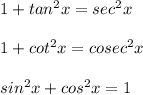
Lets solve the bottom most part first:

`1-(1)/(1-sec^2x) \\\\`

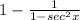
Take LCM

`1-(1)/(1-sec^2x) \\\\(1-sec^2x-1)/(1-sec^2x) \\\\(-sec^2x)/(1-sec^2x) \\\\(-(1+tan^2x))/(-tan^2x)`

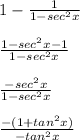
now break the LCM

`(-1)/(-tan^2x)+(-tan^2x)/(-tan^2x)\\\\(1)/(tan^2x)+1\\\\cot^2x+1`

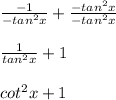
because 1/tan = cot x

and furthermore,

`cot^2x+1\\cosec^2x`

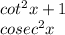
now we solve the above part and replace the bottom most part that we solved with
`cosec^2x`

`(1)/(1-(1)/(cosec^2x) ) \\\\(1)/(1-sin^2x) \\\\(1)/(cos^2x)\\\\sec^2x`

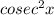
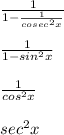
Hence proved! :D