Answer:
a)
 , b) $101
, b) $101
Explanation:
Hermes: 8 envelopes, $218
Apollo: 5 envelopes, $521
If x is the amount in each envelope, H is the amount Hemes has and A is the amount Apollo has, this would be a possible system of equations.
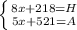
If Apollo and Hermes both had the same amount of total money, A and H could equal y

We want to find the amount in each envelope (x), so we can substitute y in the first equation for y in the second equation:
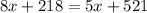
Subtract
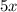 from both sides
from both sides

Subtract 218 from both sides
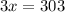
Divide both sides by 3
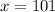
So there would have to be $101 in both envelopes for Apollo and Hermes to have the same amount of total money.