Answer:
S = 8
Explanation:
An infinite geometric series is defined as limit of partial sum of geometric sequences. Therefore, to find the infinite sum, we have to find the partial sum first then input limit approaches infinity.
However, fortunately, the infinite geometric series has already set up for you. It’s got the formula for itself which is:
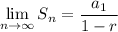
We can also write in summation notation rather S-term as:
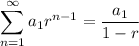
Keep in mind that these only work for when |r| < 1 or else it will diverge.
Also, how fortunately, the given summation fits the formula pattern so we do not have to do anything but simply apply the formula in.

Therefore, the sum will converge to 8.
Please let me know if you have any questions!