Question

Hey please help! its supposed to be in point-slope form ! <33

Answer 1

`y+3=-2(x-5)`

Explanation:

We need an equation of the line perpendicular to the given line

`y=(1)/(2)x+4`

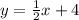
if we compare this equation with the standard form:

`y=mx+c`

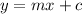
m equals 1/2 and c=4 , we do not c (y-intercept) in our calculation so just ignore it.

Furthermore the slope of the perpendicular line is given by the formula:

`m_1m_2=-1\\`

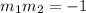
where our
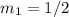`m_1=1/2` and m2 is the slope of the perpendicular line so,

`m_1m_2=-1\\\\(1)/(2) m_2=-1\\\\m_2=-2`

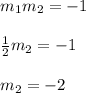
we have the slope of the perpendicular line which is -2 and the point P is given to us which is (5,-3) , so we use the equation of point-slope form:

`y-y_1=m(x-x_1)\\y-(-3)=-2(x-5)\\y+3=-2x+10\\y=-2x+7\\`

we need our answer in point-slope form so it would be

`y+3=-2(x-5)`