Question

The cylinder and cone have the same radius and height.

The Total Volume is 500cm^3.
What is the Volume of the Cylinder?
What is the Volume of each Cone?

Answer 1

Volume of Cylinder = 300cm^3, Volume of 1 Cone = 100cm^3

Explanation:

Let r be the radius

Let h be the Height

Given r = h, we will take h as r.

Volume of cylinder
`\pi r^(2) h\\=\pi r^(2) (r)\\=\pi r^(3)`

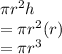
Volume of 2 cones
`2(\pi r^(2) (h)/(3) )\\=2(\pi r^(2) (r)/(3) )\\= 2((\pi r^(3) )/(3) )\\=(2)/(3) \pi r^(3)`

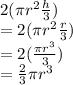
Given Total Volume = 500cm^3 = Volume of cylinder + Volume of 2 cones

`\pi r^(3) + (2)/(3)\pi r^(3) = 500 \\(5)/(3) \pi r^(3) = 500\\\pi r^(3) = 500*(3)/(5) \\\pi r^(3) = 300\\r^(3) = (300)/(\pi ) \\r=\sqrt[3]{(300)/(\pi ) } cm \\`

Now we got r and r=h,

Volume of Cylinder
`\pi (\sqrt[3]{(300)/(\pi ) } )^(3)\\=\pi ((300)/(\pi ) )\\= 300cm^(3)`

Volume of 1 cone = (Total Volume - Volume of Cylinder) / 2

= (500-300)/2

= 200/2

= 100cm^3