Question

What is the distance between a 900 kg compact car and a 1600 kg pickup truck if the gravitational force between them is about 0.0001 N?

Answer 1

The distance between the compact car and pickup truck is 0.96048 m

Step-by-step explanation:

The gravitational force is directly proportional to the product of the masses of the interacting object, it is also inversely proportional to the square of the distance between them. This is shown in equation 1;

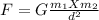`F =G (m_(1) X m_(2) )/(d^(2) )`............ 1

Where F is the gravitational force = 0.0001 N

G is the gravitational constant = 6.673 x
`10^(-11) Nm^(2) kg^(-2)`

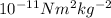
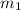`m_(1)` is the mass of the compact car = 900kg

`m_(2)` is the mass of the pickup truck = 1600kg

d is the distance and its unknown ?

Let us make d the subject formula in equation 1

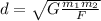`d = \sqrt{G(m_(1) m_(2) )/(F ) }` .... 2

Substituting into equation 2 we have

`d = \sqrt{(6.673x10^(-11) x 900 x 1600)/(0.0001N) }`

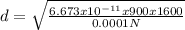
d = 0.96048m

Therefore the distance between the compact car and pickup truck is 0.96048 m

Answer 2

The distance is 0.96m

Step-by-step explanation:

Given

m1= 900kg

m2= 1600kg

Force F= 0.0001nN

G=6.67430*10^-11 Nm^2/kg^2

Required

The distance r

Step two:

the formula for the force is given as

F = Gm1m2/r2

make r subject of the formula

`r= \sqrt{(Gm1m2)/(F) }`

`r= \sqrt{(6.67430*10^-11*900*1600)/(0.0001) }\\\\r= 0.00009610992/0.0001`}\\\\r= 0.96m`

Answer:

The distance is 0.96m

Step-by-step explanation:

Given

m1= 900kg

m2= 1600kg

Force F= 0.0001nN

G=6.67430*10^-11 Nm^2/kg^2

Required:

The distance r

Step two:

the formula for the force is given as

F = Gm1m2/r2

make r subject of the formula

`r= \sqrt{(Gm1m2)/(F) }`

`r= \sqrt{(6.67430*10^-11*900*1600)/(0.0001) }\\\\r= 0.00009610992/0.0001`}\\\\r= 0.96m`