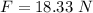Answer:
The force is
Step-by-step explanation:
From the question we are told that
The number of liquids is n = 3
The volume of the first liquid is
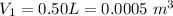
The density of the first liquid is

The volume of the second liquid is
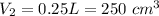
The density of the second liquid is
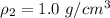
The volume of the third liquid is
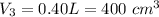
The density of the third liquid is
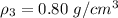
Generally the force at the bottom of the container is mathematically represented as

Here
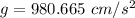
Here
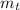 is the total mass of all the liquid which is mathematically represented as
is the total mass of all the liquid which is mathematically represented as
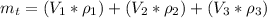
=>
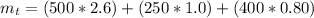
=>
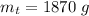
So
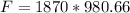
=>
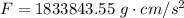
=>
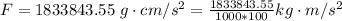
=>