Question

Consider a 0.10 M solution of a weak polyprotic acid (H2A) with the possible values of Ka1 and Ka2 given below. Calculate the contributions to [H3O+] from each ionization step. Ka1=1.0×10−4;Ka2=5.0×10−5

Answer 1

The first dissociation occurred at 0.00311 M and the second at 0.0000484 M.

Step-by-step explanation:

From the given information:

The ICE table can be computed as follows:

H2A → HA⁻ + H⁺

Initial 0.10 0 0

Change -x x x

Equilibrium 0.10 - x x x

`Ka_1 = ([HA^-][H^+])/([H_2A])`

`1.0* 10^(-4)= ([x][x])/([0.10-x])`

`1.0* 10^(-4)= ((x)^2)/((0.10-x))`

By solving for x;

x² = (1.0 × 10⁻⁴ × 0.1)

x =
`\sqrt{1* 10^(-5)}`

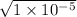
x = [H⁺] =[HA⁻] = 0.00311 M

The acid then further its dissociation again, So;

The ICE table can be computed as follows:

HA⁻ → A⁻ + H⁺

Initial 0.00311 0 0.00311

Change -x x x

Equilibrium 0.00311 - x x 0.00311 + x

`Ka_2 = ([A^-][H^+])/([HA])`

`5.0 * 10^(-5) = ((0.00311+x)x)/((0.00311-x))`

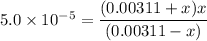
By solving for x;

x = [H⁺] = 0.0000484 M

Therefore, the first dissociation occurred at 0.00311 M and the second at 0.0000484 M.