Question

For a soccer practice, the coach set up four cones, labeled W, X, Y, and Z, to mark the edges of the rectangular field. Suppose the field is drawn on a coordinate plane, where the x- and y-values represent the position, in yards, from the center of the field, which is located at (0, 0). The location of the cones are as follows. Cone W is located at (-38, -53). Cone X is located at (-38, 53). Cone Y is located at (38, 53). Cone Z is located at (38, -53). What is the perimeter of the field? A. 364 yards B. 8,056 yards C. 182 yards D. 38 yards

Answer 1

A. 364 yards

Explanation:

The distance between two points
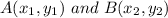`A(x_1,y_1)\ and\ B(x_2,y_2)` on the coordinate plane is given as:

`|AB|=√((x_2-x_1)^2+(y_2-y_1)^2)`

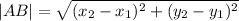
The cone W, X, Y and Z form a rectangle.

The perimeter for the rectangle = 2(length + breadth)

`Length=|WX|=√((-38-(-38))^2+(53-(-53))^2)=106 \\\\Breadth=|XY|=√((38-(-38))^2+(53-53)^2)=76`

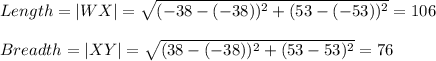
Perimeter = 2(length + breadth) = 2(106 + 76) = 364 yards