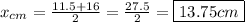Hi there!
a)
Since the objects are made of material of a constant area/mass density, we can simplify the process.
To calculate the value of the y-coordinate for the center of mass, we can begin by finding the y-coordinates for the center of masses for both rectangles.
Also, let the small rectangle be 'Rectangle 1', and the bigger rectangle 'Rectangle 2'.
Smaller rectangle:
Since D = 9 cm and B = 32 cm, the remaining width of the small rectangle is equal to B - D = 32 - 9 = 23 cm. The midpoint of this width is:

Now, the height of this rectangle is 10 cm. The midpoint of this height is 10/2 = 5 cm. However, this is not the actual y-coordinate. Since the height of the block below is 5 cm, we must add the two because this rectangle is on top of the other.
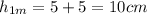
Larger rectangle:
We can simply take the midpoints of its dimensions to solve for its center of mass.

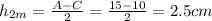
Now, take the averages of the coordinates for both rectangles to solve.
y-coordinate:
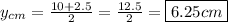
x-coordinate: