Question

A boat travels with velocity vector (25, 25 StartRoot 3 EndRoot). What is the directional bearing of the boat? N 30° E E 30° S E 30° N N 30° W

Answer 1

A) N 30 E

Explanation:

Answer 2

The directional bearing of the boat is N 30º E

Explanation:

Let
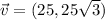`\vec v = (25, 25√(3))`, where
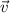`\vec v` is the vector velocity. Given that such vector is represented in rectangular, a positive value in the first component is the value of the vector in the east direction, whereas a positive value in the second component is in the north direction. The directional bearing of the boat (
`\theta`), measured in sexagesimal degrees, is determined by trigonometrical means:

`\theta = \tan^(-1)(v_(y))/(v_(x))` (1)

If we know that
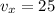`v_(x) = 25` and
`v_(y) = 25√(3)`, then the directional bearing of the boat is:

`\theta = \tan^(-1) √(3)`

`\theta = 60^(\circ)`

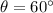
In consequence, we conclude that the direction bearing of the boat is 30 degrees to the East from the North (N 30º E).