Question

simplify the expression below and state the value of m for which the simplified expression is not defined 2m² + m - 15/ m² - 9​

Answer 1

• The simplified expression is:
  `(2m-5)/(m-3)`

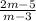
• The simplified expression is undefined for m=3

Step-by-step explanation:

The given expression is:

`(2m^2+m-15)/(m^2-9)`

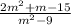
The numerator can be siplified by using factorization and denominator will be simplified using the formula

`a^2-b^2 = (a+b)(a-b)`

So,

`= (2m^2+6m-5m-15)/((m)^2-(3)^2)\\=(2m(m+3)-5(m+3))/((m-3)(m+3))\\=((2m-5)(m+3))/((m-3)(m+3))\\=(2m-5)/(m-3)`

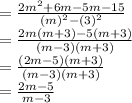
A fraction is undefined when the denominator is zero. In order to find the value of m on which the simplified fraction will be undefined we will put denominator equal to zero.

So,

`m-3 = 0 => m = 3`

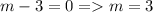
Hence,

• The simplified expression is:
  `(2m-5)/(m-3)`

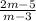
• The simplified expression is undefined for m=3