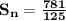Question

What is the sum of the first five terms of the geometric sequence in which a1=5 and r=1/5

express your answer as an improper fraction.

Answer 1

Sum of the first five terms of the geometric sequence in which a1=5 and r=1/5 is
`\mathbf{S_n=(781)/(125) }`

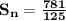
Explanation:

We need to find sum of the first five terms of the geometric sequence in which a1=5 and r=1/5

The formula used to find sum of the geometric sequence is:
`S_n=(a(r^n-1))/(r-1)`

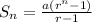
Where a is the first term, r is the common ratio and n is the number of terms

Now finding sum of the first five terms of the geometric sequence

We have a=5, r=1/5 and n=5

Putting values in the formula:

`S_n=(a(r^n-1))/(r-1)\\S_n=(5(((1)/(5)) ^5-1))/((1)/(5)-1)\\S_n=(5((1)/(3125)-1))/((1-5)/(5))\\S_n=(5((1-3125)/(3125)))/((-4)/(5))\\S_n=(5((-3124)/(3125)))/((-4)/(5))\\S_n=5((-3124)/(3125))}*{(-5)/(4)}\\S_n=(781)/(125)`

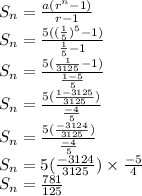
So, sum of the first five terms of the geometric sequence in which a1=5 and r=1/5 is
`\mathbf{S_n=(781)/(125) }`