Question

Use f(x)=5x+2 and g(x)=3-x. what is the value of f(g(-1)) and g(f(-1))?

Answer 1

f(g(-1)) = 22

g(f(-1))=6

Explanation:

We are given

`f(x)=5x+2 \\g(x)=3-x`

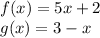
We need to find f(g(-1)) and g(f(-1))

Finding f(g(-1))

First we will find f(g(x)) i.e

`f(g(x))=5(3-x)+2\\f(g(x))=15-5x+2\\f(g(x))=-5x+17`

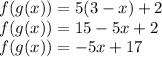
Now finding f(g(-1)) by putting x=-1

`f(g(x))=-5x+17\\Put \ x=-1\\f(g(-1))=-5(-1)+17\\f(g(-1))=5+17\\f(g(-1))=22`

So, f(g(-1)) = 22

Finding g(f(-1))

First we will find g(f(x)) i.e

`g(f(x))=3-(5x+2)\\g(f(x))=3-5x-2\\g(f(x))=-5x+1`

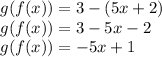
Now finding g(f(-1)) by putting x=-1

`g(f(x))=-5x+1\\Put \ x = -1\\g(f(-1))=-5(-1)+1\\g(f(-1))=5+1\\g(f(-1))=6`

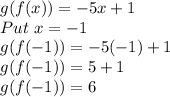
So, g(f(-1))=6