Question

Learning task 2

A. Solve the systems of equations by a) graphing b) elimination c) substitution
Eq. 1: 2x - 3y = -1; Eq. 2: y = x - 1
B. Solve the problem using any method.
The sum of two numbers is 32 and the difference is 2. Find the numbers​

Answer 1

The given equations are

`2x-3y=-1\cdots(i) \\\\y=x-1\cdots(ii)`

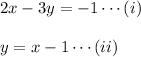
(a) Solution by graphing both the equations:

Graph for both the equations (i) and (ii) are in the figure. The point of intersection of both the graph is the solution of the equations.

From the graph, the point of intersection is (4,3)).

Hence, the required solution is (4,3).

(b) Solution by elimination method:

Equations (ii) can be written as -x+y=-1, now multiply it by 2, we have

`-2x+2y=-2\cdots(iii)`

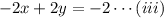
Add equations (i) and (iii), we have

2x-3y=-1

-2x+2y=-2

__________

`\Rightarrow -3y+2y=-1-2\\\\ \Rightarrow -y=-3\\\\ \Rightarrow y=3.`

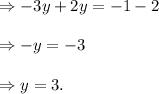
Putting the value of y=3 in equation (i), we have

`2x-3* 3=-1 \\\\\Rightarrow 2x=-1+9=8 \\\\\Rightarrow x=8/2=4`

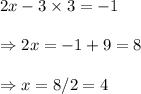
Hence, the required solution is (4,4).

(c) Solution by substitution method:

Substituting the value of y from equation (ii) to equation (i), we have

`2x-3(x-1)=-1 \\\\\Rightarrow 2x-3x+3=-1 \\\\\Rightarrow -x=-1-4=-4 \\\\\Rightarrow x=4`

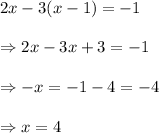
Putting the value of x=4 in equation (i), we have

`y=4-1=3`.

Hence, the required solution is (4,3).