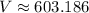Question

A cone has a base of
`5.4` and a height of
`8`. The diameter is
`6`. What is the volume? If you were to dilate the cone with a scale factor of
`2`, what would the new radius be?

Answer 1

(I) V = 24π ≈ 75.3982 units³

(II) V = 192π ≈ 603.186 units³

General Formulas and Concepts:

Math - Symbols

• π - pi, the number 3.1415926535897932384626433832795

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Geometry

• Dilations
• Diameter: d = 2r
• Volume of a Cone:
  `V= (1)/(3) \pi r^2h`

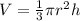
Explanation:

Step 1: Define

Height h = 8

Diameter d = 6

Base b = 5.4 (not needed in calculations)

Step 2: Find radius r

1. Substitute: 6 = 2r
2. Isolate r: 3 = r
3. Rewrite: r = 3

Step 3: Find V of Normal Dimensions

1. Substitute:
   `V= (1)/(3) \pi (3)^2(8)`
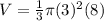
2. Exponents:
   `V= (1)/(3) \pi (9)(8)`
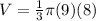
3. Multiply:
   `V= 24 \pi`
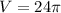
4. Evaluate:
   `V \approx 75.3982`

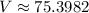
Step 4: Find Dilations

Scale Factor: 2

1. Define radius: r = 3
2. Dilate: r' = 3(2)
3. Multiply: r' = 6

1. Define height: h = 8
2. Dilate: h' = 8(2)
3. Multiply: h' = 16

Step 5: Find V of Dilated Dimensions

1. Substitute:
   `V= (1)/(3) \pi (6)^2(16)`
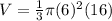
2. Exponents:
   `V= (1)/(3) \pi (36)(16)`
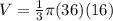
3. Multiply:
   `V= 192 \pi`
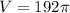
4. Evaluate:
   `V \approx 603.186`