Question

A family wants to build a rectangular garden on one side of a barn. If 600 feet of fencing is available to use, then what is the area of the largest garden that could be built?

(A) Define a function that relates the area enclosed by the fence (in 〖ft.〗^2) in terms of its length (in ft.)
(B) What is the practical domain of this function?
(C) What is the largest area that the fence could enclose?

Answer 1

Answer: (A)
`A=300l-l^(2)`

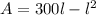
(B) Length varies between 1 and 150

(C) Largest area is 22500ft²

Explanation: Suppose length is l and width is w.

The rectangular garden has perimeter of 600ft, which is mathematically represented as

`2l+2w=600`

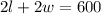
Area of a rectangle is calculated as

`A=lw`

Now, we have a system of equations:

`2l+2w=600`

`A=lw`

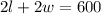
Isolate w, so we have l:

`2w=600-2l`

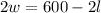
w = 300 - l

Substitute in the area equation:

A = l(300 - l)

A = 300l - l²

(A) Function of area in terms of length is given by A = 300l - l²

(B) The practical domain for this function is values between 1 and 150.

(C) For the largest area, we need to determine the largest garden possible. For that, we take first derivative of the function:

A' = 300 - 2l

Find the values of l when A'=0:

300 - 2l = 0

2l = 300

l = 150

Replace l in the equation:

w = 300 - 150

w = 150

Now, calculate the largest area:

A = 150*150

A = 22500

The largest area the fence can enclose is 22500ft².