It looks like the differential equation is
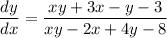
Factorize the right side by grouping.
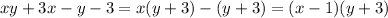
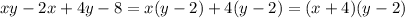
Now we can separate variables as
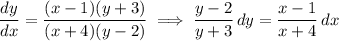
Integrate both sides.
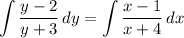

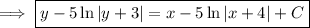
You could go on to solve for
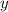 explicitly as a function of
explicitly as a function of
 , but that involves a special function called the "product logarithm" or "Lambert W" function, which is probably beyond your scope.
, but that involves a special function called the "product logarithm" or "Lambert W" function, which is probably beyond your scope.