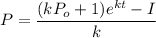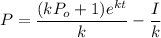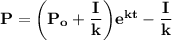Question

Suppose a country's population at any time t grows in accordance with the rule dP dt = kP + I where P denotes the population at any time t, k is a positive constant reflecting the natural growth rate of the population, and I is a constant giving the (constant) rate of immigration into the country. If the total population of the country at time t = 0 is P0, find an expression for the population at any time t.

Answer 1

`\mathbf{P =\bigg (P_o +( I)/(k) \bigg)e^(kt)- (I)/(k)}`

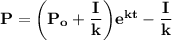
Explanation:

Given that:

A country population at any given time (t) is:

`(dP)/(dt)= kP+I`

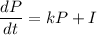
where;

P = population at any time t

k = positive constant

I = constant rate of immigration into the country.

Using the method of separation of the variable;

`(dP)/(kP+1)= dt`

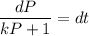
Taking integration on both sides:

`\int (dP)/(kP+I)= \int \ dt`

`(1)/(k) log (kP + I) = t+c_1 \ \ \ here: c_1 = constant \ of \ integration`

`log (kP + I) =k t+kc_1`

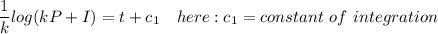
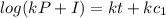
By applying the exponential on both sides;

`e^(log (kP + I) )=e^(k t+kc_1 )`

`KP+I = e^(kt) *e^(kc_1)`

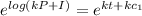
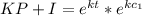
Assume
`e^(kc_1 )= C`

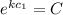
Then:

`kP + I = Ce^(kt)`

`kP = Ce^(kt)-I`

`P =( Ce^(kt)-I)/(k) \ \ \---- Let \ that \ be \ equation \ (1)`

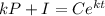
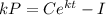
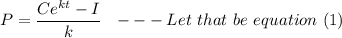
When time t = 0, The Total population of the country is also
`P_o`

`P_o = (Ce^(0(t)) -I)/(k)`

`P_o = (Ce^(0) -I)/(k)`

`P_o = (C-I)/(k)`

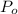
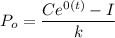
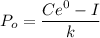
C - I = kP₀

C = kP₀ + I

Substituting the value of C back into equation(1), we have:

`P =( (kP_o+1)e^(kt)-I)/(k)`

`P =( (kP_o+1)e^(kt))/(k) - (I)/(k)`

`\mathbf{P =\bigg (P_o +( I)/(k) \bigg)e^(kt)- (I)/(k)}`