Question

Suppose that the separation between two speakers A and B is 6.60 m and the speakers are vibrating in-phase. They are playing identical 126-Hz tones and the speed of sound is 343 m/s. An observer is seated at a position directly facing speaker B in such a way that his line of sight extending to B is perpendicular to the imaginary line between A and B. What is the largest possible distance between speaker B and the observer, such that he observes destructive interference

Answer 1

Complete question

The diagram for this question is shown on the first uploaded image

Answer:

The largest possible distance is
`e = 15.33 \ m`

Step-by-step explanation:

From the question we are told that

The separation between Speaker at position A and B is AB = 6.60 m

The frequency of the tune which the speaker are playing is
`f = 126 \ Hz`

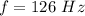
The speed of sound is
`v = 343 \ m/s`

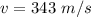
Generally the wavelength of the tune playing is mathematically represented as

`\lambda = (v)/(f)`

=>
`\lambda = (343)/( 126)`

=>
`\lambda = 2.72 \ m`

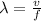
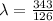
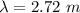
Let the observer be at position D

Generally the distance A and is mathematically evaluated using Pythagoras theorem as

`AC = √(AB ^2 + BC^2)`

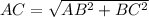
Let BC = e

So

`AC = √(6.60 ^2 + e^2)`

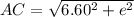
Generally the path difference between the first and the second speaker from the observer point of view is mathematically represented as

`P = AC - BC`

=>
`P = √(6.60 ^2 + e^2) - e`

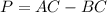
Generally the condition for destructive interference is mathematically represented as

`P = (2n - 1 )(\lambda)/(2)`

Here n is the order of the fringe which is one

=>
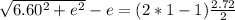
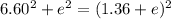
`√(6.60 ^2 + e^2) - e = (2 * 1 - 1 )(2.72)/(2)`

=>
`√(6.60 ^2 + e^2) - e = 1.36`

=>
`6.60 ^2 + e^2 =( 1.36 +e)^2`

=>
`6.60 ^2 + e^2 =1.8496 + 2.72e +e^2`

=>
`e = 15.33 \ m`