Question

A line segment AB has the coordinates A (2,3) AND B ( 8,11) answer the following questions (1) What is the slope of AB? (2) What is the length of AB? (3) What are the coordinates of the mid point of AB?(4) What is the slope of a line perpendicular to AB ?

Answer 1

1) The slope of the line segment AB is
`(4)/(3)`.

2) The length of the line segment AB is 10.

3) The coordinates of the midpoint of the line segment AB is
`M(x,y) = (5,7)`.

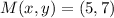4) The slope of a line perpendicular to line segment AB is
`-(3)/(4)`.

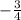Explanation:

1) Let
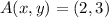`A(x,y) = (2,3)` and
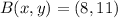`B(x,y) = (8,11)`. From Analytical Geometry, we get that slope of AB (
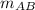`m_(AB)`), dimensionless, is determined by the following formula:

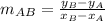`m_(AB) = (y_(B)-y_(A))/(x_(B)-x_(A))` (1)

If we know that
`x_(A) = 2`,
`x_(B) = 8`,
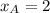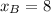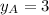`y_(A) = 3` and
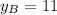`y_(B) = 11`, the slope of the line segment is:

`m_(AB) = (11-3)/(8-2)`

`m_(AB) = (4)/(3)`

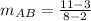
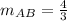
The slope of the line segment AB is
`(4)/(3)`.

2) The length of the line segment AB (
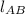`l_(AB)`), dimensionless, can be calculated by the Pythagorean Theorem:

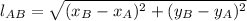`l_(AB) =\sqrt{(x_(B)-x_(A))^(2)+(y_(B)-y_(A))^(2)}` (2)

If we know that
`x_(A) = 2`,
`x_(B) = 8`,
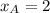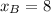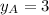`y_(A) = 3` and
`y_(B) = 11`, the length of the line segment AB is:

`l_(AB) = \sqrt{(8-2)^(2)+(11-3)^(2)}`

`l_(AB) = 10`

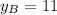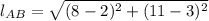
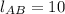
The length of the line segment AB is 10.

3) The coordinates of the midpoint of the line segment AB are, respectively:

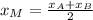`x_(M) = (x_(A)+x_(B))/(2)` (3)

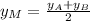`y_(M) = (y_(A)+y_(B))/(2)` (4)

If we know that
`x_(A) = 2`,
`x_(B) = 8`,
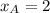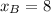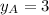`y_(A) = 3` and
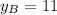`y_(B) = 11`, the coordinates of the midpoint of the line segment AB are, respectively:

`x_(M) = (2+8)/(2)`

`x_(M) = 5`

`y_(M) = (3+11)/(2)`

`y_(M) = 7`

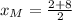
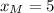
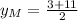
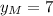
The coordinates of the midpoint of the line segment AB is
`M(x,y) = (5,7)`.

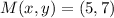4) From Analytical Geometry we can determine the slope of a line perpendicular to line segment AB as a function of the slope of the line segment:

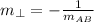`m_(\perp) = -(1)/(m_(AB))` (5)

If we know that
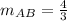`m_(AB) = (4)/(3)`, then the slope of a line perpendicular to AB is:

`m_(\perp) = - (1)/((4)/(3) )`

`m_(\perp) = -(3)/(4)`

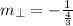
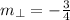
The slope of a line perpendicular to line segment AB is
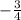`-(3)/(4)`.