Answer:
Explanation:
As it is a second order equation, it means that it has two possible answers and they are
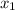 and
and
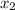 .
.
The famous quadratic formula for solving any second order equation is the following:
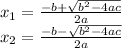
Where a is the coefficient of
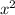 , b is the coefficient of x, and c is the free term. In other words,
, b is the coefficient of x, and c is the free term. In other words,
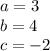
as the equation should be in the following form:
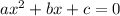
Therefore the possible answer should be the following,
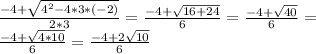
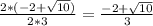
by dividing the numerator and denominator by 2, we can deduce the following,