Question

Triangle ABC is a right triangle. The length of the legs are 3 in and 6 in, how long is the hypotenuse? (Round to the nearest tenth if necessary)

A) 3.3 in
B) 6.7 in
C) 7.9 in
D) 9.0 in

Answer 1

Answer: A

Explanation:

Use Pythagorean Theorem in order to solve this:

`a^(2) + b^(2) = c^(2)`

(c is the hypotenuse)

So that would be:

`3^(2) + 6^(2) = c^(2)`

If you solve this, you would find that:

`c^(2) = 45`

`c = 3√(5)`

Answer = B

Answer 2

Triangle ABC is a right triangle. The length of the legs are 3 in and 6 in, how long is the hypotenuse? (Round to the nearest tenth if necessary)

When the two legs are given, the hypotenuse is found by using the Pythagorean Theorem, which states that:

`\displaystyle a^(2) +b^(2) =c^(2)`

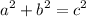
In the theorem, a and b are the two legs, and c is the hypotenuse. Since you are given the length of the two legs, substitute it into the equation.

`a=3\\b=6`

`3^(2) +6^(2)=c^(2)`

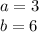
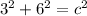
Now, you need to square both 3 and 6. When you square a number, you're basically multiplying the number by itself.

`3^(2) =3 * 3=9\\6^(2)=6 * 6=36`

Substitute the numbers into the equation.

`9+36=c^(2)`

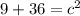
Add:

`45=c^(2)`

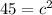
You're looking for the value of c, not c squared. To remove the square, you need to square root it.

`\displaystyle √(45)=\sqrt{c^(2) }`

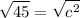
Using a calculator, find the square root of 45.

`\displaystyle √(45)=\sqrt{c^(2) }\\c \approx 6.7`

The answer to your question is B) 6.7 inches.