Question

Fine the distance between (-8, 4) and (-8, -2)

Answer 1

The distance between the two points is six units.

Explanation:

We are given two coordinate pairs:

• (-8, 4)
• (-8, -2)

With these, we can find the distance between the two using the distance formula. The distance formula is:

`\displaystyle d = √((x_2-x_1)^2+(y_2-y_1)^2), \ \text{where d is the distance.}`

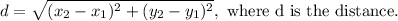
Additionally, we need to label our coordinates. In math, coordinates are labeled as (x₁, y₁) and (x₂, y₂).

Therefore, our coordinate pairs can be labeled in this format.

(-8, 4)

• x₁ = -8
• y₁ = 4

(-8, -2)

• x₂ = -8
• y₂ = -2

Now, we can substitute these values into the formula and solve for d.

`\displaystyle d = √((x_2-x_1)^2+(y_2-y_1)^2)\\\\d = √((-8 - -8)^2 + (-2 - 4)^2)\\\\d = √((0)^2+(-6)^2)\\\\d = √(0 + 36)\\\\d = √(36)\\\\d = 6`

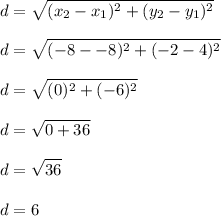
Therefore, the distance between the two points is six units.