Question

8. A carpenter balances his daily projects between small jobs (x) and building cabinets (y). He allots 2

hours per small job and 4 hours per cabinet job. He works at most 12 hours per day (2x + 4y <_12).
He cannot do more than 3 small jobs per day
and get all of his cabinets done (Y >_0) & (0 The carpenter earns $125 per small job and $500 per cabinet job. Find a combination of small jobs and
completed cabinet jobs per week that will maximize income.

Answer 1

`\$1125`

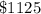
Explanation:

The equations of the system are

`2x+4y\leq 12`

`y\geq 0`

`0<x\leq 3`

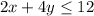
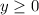
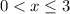
From the graph it can be seen that points
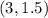`(3,1.5)` and
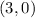`(3,0)` falls in the bounded region.

The income will be

`125x+500y=125* 3+500* 1.5\\ =\$1125`

`125* 3+500* 0=\$375`

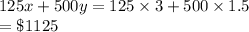
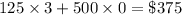
So, the person can do 3 small jobs and build 1 and a half cabinets per day.

The maximum income will be
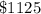`\$1125`.