Question

A line includes the points (-39,49) and (0,0). What is its equation in slope-intercept form?

Answer 1

The equation in the slope-intercept form will be:

`y=-(49)/(39)x+0`

Explanation:

Given the points

• (-39,49)

• (0,0)

Finding the slope between the points using the formula

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(-39,\:49\right),\:\left(x_2,\:y_2\right)=\left(0,\:0\right)`

`m=(0-49)/(0-\left(-39\right))`

`m=-(49)/(39)`

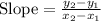
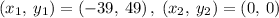
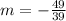
We know that the point-slope of the line equation is

`y-y_1=m\left(x-x_1\right)`

substituting
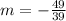`m=-(49)/(39)` and (-39,49) in the equation

`y-y_1=m\left(x-x_1\right)`

`y-49=(-49)/(39)\left(x-\left(-39\right)\right)`

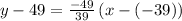
Now writing the equation in slope-intercept form

`y=mx+b`

where m is the slope and b is the y-intercept

`y-49=(-49)/(39)\left(x-\left(-39\right)\right)`

`y-49=(-49)/(39)\left(x+39\right)`

`\mathrm{Apply\:the\:fraction\:rule}:\quad (-a)/(b)=-(a)/(b)`

`y-49=-(49)/(39)\left(x+39\right)`

`\mathrm{Add\:}49\mathrm{\:to\:both\:sides}`

`y-49+49=-(49)/(39)\left(x+39\right)+49`

`y=-(49)/(39)x+0` ∵
`y=mx+b`

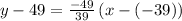
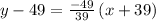
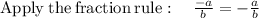
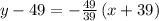
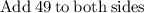
Where

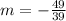`m=-(49)/(39)` and the y-intercept i.e.
`b=0`

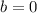
Therefore, the equation in the slope-intercept form will be:

`y=-(49)/(39)x+0`