Question

Find the coordinates of point P along the directed line segment AB so that AP to PB is the given ratio. A(10, 8), B(18, 12); 1 to 3

Answer 1

The coordinates of P are (12,9)

Explanation:

Equations

We are given the endpoints of the segment AB: A(10,8) B(18,12).

It's required to find the coordinates of point P(x,y) along the segment AB such that:

`\displaystyle (AP)/(PB)=(1)/(3)`

The ratio of the distances is the same as the ratio of their respective coordinates:

`\displaystyle (x_(AP))/(x_(PB))=(1)/(3)`

`\displaystyle (y_(AP))/(y_(PB))=(1)/(3)`

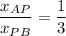
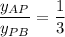
Since

`x_(AP)=x_P-x_A=x-10`

`x_(PB)=x_B-x_P=18-x`

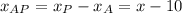
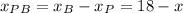
Then:

`\displaystyle (x-10)/(18-x)=(1)/(3)`

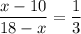
Multiplying by 3 (18-x):

3( x - 10 )= 18 - x

3x - 30 = 18 - x

Adding x and 30:

4x = 48

x = 12

Similarly:

`\displaystyle (y-8)/(12-y)=(1)/(3)`

Multiplying by 3 (12-y):

3( y - 8 ) = 12 - y

3y - 24 = 12 - y

Adding y and 24:

4y = 36

y = 9

The coordinates of P are (12,9)