Question

What is the area of a circle with a radius of 4 cm? Use 3.14 for pi and round to the nearest hundredth. Answer value

Answer 1

`\textit{area of a circle}\\\\A=\pi r^2~~\begin{cases}r=radius\\[-0.5em]\hrulefill\\r=4\end{cases}\implies A=\pi (4)^2\implies \stackrel{using~\pi =3.14}{A=50.24}`

Answer 2

The area of circle is 50.24 cm².

Step-by-step Step-by-step explanation:

Here's the required formula to find the area of circle :

`\longrightarrow{\sf{\pmb{Area_((Circle)) = \pi{r}^(2)}}}`

• π = 3.14
• r = radius

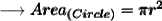
Substituting all the given values in the formula to find the area of circle :

`\longrightarrow{\sf{Area_((Circle)) = \pi{r}^(2)}}`

`\longrightarrow{\sf{Area_((Circle)) = 3.14{(4)}^(2)}}`

`\longrightarrow{\sf{Area_((Circle)) = (314)/(100){(4 * 4)}}}`

`\longrightarrow{\sf{Area_((Circle)) = (314)/(100){(16)}}}`

`\longrightarrow{\sf{Area_((Circle)) = (314)/(100) * 16}}`

`\longrightarrow{\sf{Area_((Circle)) = (5024)/(100)}}`

`\longrightarrow{\sf{\underline{\underline{\red{Area_((Circle)) = 50.24 \: {cm}^(2)}}}}}`

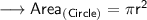
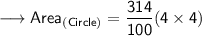
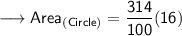
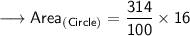
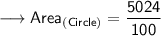
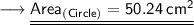
Hence, the area of circle is 50.24 cm².

`\rule{300}{2.5}`