Question

3. According to The Motorist, a publication of the American Automobile Association, 90% of all calls for emergency

Service on a cold winter day in Tottenville are for cars that won't start because of a dead battery, 10% of the calls a
cars that won't start because they have no gas, and 4% of the calls are for cars that won't start because of a dead
battery and no gas. If a typical call is randomly selected, what is the probability that it is for a car that won't start
because of a dead battery or because of no gas?

Answer 1

The probability that a randomly selected call is for a car that won't start because of dead battery or because of no gas is 0.96

Explanation:

The percentage of calls for emergency due to dead battery = 90%

The percentage of calls for emergency due to no gas = 10%

The percentage of calls for emergency due to dead battery and no gas = 4%

Therefore;

The probability that a call for a car that won't start because of dead battery, P(B) =
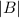`\left | B \right |` = 0.9

The probability that a call for a car that won't start because of no gas, P(N) =
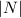`\left | N \right |` = 0.1

The probability that a call for a car that won't start because of dead battery and no gas, P(B∩N) =
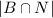`\left | B \cap N \right |` = 0.04

Therefore, the probability that a randomly selected call is for a car that won't start because of dead battery or because of no gas is given as follows;

`\left | B \cup N \right | = \left | B \right | + \left | N \right | - \left | B\cap N \right |`

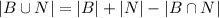
Where;

Therefore, we have;

`\left | B \cup N \right |` = The probability that a randomly selected call is for a car that won't start because of dead battery or because of no gas

Substituting gives;

`\left | B \cup N \right |` = 0.9 + 0.1 - 0.04 = 0.96

∴ The probability that a randomly selected call is for a car that won't start because of dead battery or because of no gas = 0.96.