Question

There is a bag filled with 4 blue, 3 red and 5 green marbles.

A marble is taken at random from the bag, the colour is noted and then it is replaced.
Another marble is taken at random.
What is the probability of exactly 1 red?

Answer 1

There are four possible outcomes two reds, red then not red, not red then red, both not red.
Because the first marble is replaced P(red) is always 3/12 = 1/4 and P(not red) = 9/12 = 3/4
P(red then not red) = 1/4 x 3/4 = 3/16
P(not red then red) = 3/4 x 1/4 = 3/16
P(exactly one red) = 3/16 + 3/16 = 6/16 = 3/8

[ P(two reds) = 1/4 x 1/4 = 1/16 and P(no reds) = 3/4 x 3/4 = 9/16 so P(one red) = 1 - 1/16 - 9/16 = 6/16 = 3/8]

Answer 2

`\displaystyle(3)/(16)`

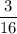
Explanation:

Probability represents the likelihood of an event occurring. Complex probability is the likelihood of a series of events occurring.

Independent Events

The question states that the marbles are replaced after being recorded. This means that the separate drawing of marbles is independent of each other. So, the probability of an event occurring does not change based on events that happened earlier.

This is important to this question because it means that probability does not change based on if the one red marble was drawn first or second.

Probability of a Red

First, we need to find the probability of drawing a red marble. Probability is represented as the number of successful outcomes (drawing a red) over the number of possible outcomes (number of marbles). Out of the total 12 marbles, 3 of them are red. So, the probability of drawing a red is
`\displaystyle(3)/(12)`.

The Complement

In probability, the complement is the likelihood of an event not occurring. So, in this situation, the complement is the likelihood of not drawing a red. Out of the total 12 marbles, 9 are NOT red. So, the complement is
`\displaystyle(9)/(12)`.

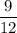Complex Probability

To find the probability of 2 different events both occurring, multiply the probabilities together.

• 
  `\displaystyle(3)/(12)*(9)/(12)=(27)/(144)`

Then, we can simplify the fraction by dividing by 9

• 
  `\displaystyle(3)/(16)`

This means that the probability of drawing exactly one red is 3/16.