Answer:
Solving the inequality
 , we get
, we get

Explanation:
We need to solve the inequality

Using the BODMAS rule, first we will solve the bracket:
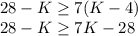
Now, we will subtract 28 from both sides
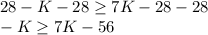
Subtracting -7k on both sides
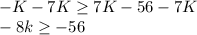
Finally, divide both sides by -8 and inverse the inequality, as we are dividing with a minus digit.
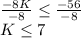
So, solving the inequality
 we get
we get
