Question

Express y = -2x² - 4x + 7 in the form of perfect square and find the maximum points.

Answer 1

Maximum: (-1,9)

Explanation:

Vertex form of the quadratic function

If the graph of the quadratic function has a vertex at the point (h,k), then the function can be written as:

`y=a(x-h)^2+k`

Where a is the leading coefficient.

We are given the following function:

`y =-2x^2-4x+7`

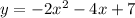
To find the vertex, we need to complete squares. First, factor -2 on the first two terms:

`y =-2(x^2+2x)+7`

The expression in parentheses must be completed to represent the square of a binomial. Adding 1 and subtracting 1:

`y =-2(x^2+2x+1- 1)+7`

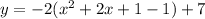
Taking out the -1:

`y =-2(x^2+2x+1)+2+7`

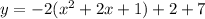
Factoring the trinomial and operating:

`y =-2(x+1)^2+9`

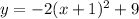
Comparing with the vertex form we have

Vertex (-1,9)

Leading coefficient: -2

Since the leading coefficient is negative, the function has a maximum value at its vertex, i.e.

Maximum: (-1,9)