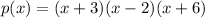Question

Khan Academy

Factor using polynomial division
The polynomial p(x) = x3 + 7x2 – 36 has a known factor of (x + 3).
Rewrite p(x) as a product of linear factors.
p(x)=

Answer 1

p(x) as a product of linear factors.
`p(x)=(x+3)(x-2)(x+6)`

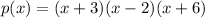
Explanation:

(x+3) is the factor of polynomial
`p(x) = x^3 + 7x^2 - 36`

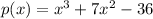
So, we can divide
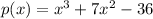`p(x) = x^3 + 7x^2 - 36` by (x+3) to find other factors

The division is shown in figure attached.

The quotient is: x^2+4x-12

Now factoring the quotient to find linear factors

`x^2+4x-12\\=x^2+6x-2x-12\\=x(x+6)-2(x+6)\\=(x-2)(x+6)`

The factors are
`(x+3)(x-2)(x+6)`

So, p(x) as a product of linear factors.
`p(x)=(x+3)(x-2)(x+6)`