Question

Given segment AB with points (-4, 8) and (6,3) respectively. Find the

coordinates of point P that partitions Segment AB in the ratio 3:2. The answer should be entered in the form (x,y) with out any spaces between characters.

Answer 1

The answer is "Coordinates of point P= (2,5)"

Explanation:

We are familiar with the internal division of AB by point P, i.e. 3:2,
`(AP)/(PB)= (3)/(2)`

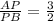
Therefore, we use the internal division formula.

Points:

`\to (-4,8) \ and \ (6,3)\\\\ x_1 = -4\\y_1 = 8\\x_2= 6\\y_2 =3 \\`

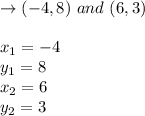
Formula:

`\to x = ((mx_2 + nx_1))/((m + n))\\\to y = ((my_2 + ny_1))/((m + n))\\\\where,\\\\\to m = 3 \\ \to n = 2`

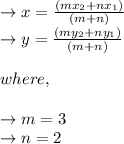
Replacing the x coordinate representations of A and B with x, we have

`x = ((3 * 6 + 2 * (-4)))/((3 + 2))\\\\`

`= ((18 - 8))/(5)\\\\ = (10)/(5)\\\\ = 2`

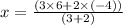
Replacing the, y coordinate representations of A and B with y, we have

`y = ((3 * 3 + 2 * 8))/((3 + 2))\\\\`

`= (( 9 +16))/((5))\\\\= (25)/(5)\\\\=5`

The coordinates of point P= (2,5).