Question

Two lines, A and B, are represented by the equations given below!

Line A: y = x - 4
Line B: y = 3x + 4
Which of the following shows the solution to the system of equations and explains why?

A. (-3,-5), because the point satisfies ONE of the equations

B. (-3,-5), because the point lies between the two axes

C. (-4,-8), because the point satisfies BOTH equations

D. (-4,-8), because the point does not lie on any axis

Answer 1

The solutions to the system of equations are:

`y=-8,\:x=-4`

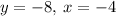
Thus, option C is true because the point satisfies BOTH equations.

Explanation:

Given the system of the equations

`\begin{bmatrix}y=x-4\\ y=3x+4\end{bmatrix}`

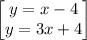
Arrange equation variables for elimination

`\begin{bmatrix}y-x=-4\\ y-3x=4\end{bmatrix}`

`y-3x=4`

`-`

`\underline{y-x=-4}`

`-2x=8`

`\begin{bmatrix}y-x=-4\\ -2x=8\end{bmatrix}`

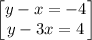
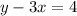
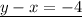
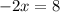
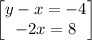
solve for x

`-2x=8`

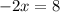
Divide both sides by -2

`(-2x)/(-2)=(8)/(-2)`

`x=-4`

`\mathrm{For\:}y-x=-4\mathrm{\:plug\:in\:}x=-4`

`y-\left(-4\right)=-4`

`y+4=-4`

`y=-8`

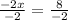
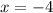
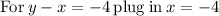
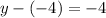
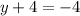
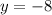
The solutions to the system of equations are:

`y=-8,\:x=-4`

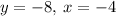
Thus, option C is true because the point satisfies BOTH equations.