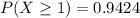Answer:
a
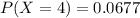
b
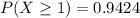
Explanation:
From the question we are told that
The probability of a US household having an internet access in 2001 is p = 0.51
The sample size is n = 4
Generally the distribution of the number of US household with internet access at 2001 follows a binomial distribution
i.e

and the probability distribution function for binomial distribution is
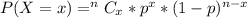
Here C stands for combination hence we are going to be making use of the combination function in our calculators
Generally the probability that all four had Internet access in 2001 is mathematically represented as
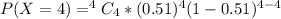
=>
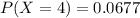
Generally the probability that at least one of four randomly selected U.S. households had Internet access in 2001 is mathematically represented as

=>
![P(X \ge 1 ) = 1- [^(4)C_0 * (0.51 )^0 * (1- 0.51 )^(4-0 ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/dlk80sys90qeuse9rv07yt5ssvzr73uw3n.png)
=>
![P(X \ge 1 ) = 1- [1 * 1 * (0.49 )^(4 ) ]](https://img.qammunity.org/2021/formulas/mathematics/college/q07cho12p5yo5xa1hyxvs1f646ka5spgnm.png)
=>