Question

How do I solve this equation and check the solutions?

Answer 1

10+√3=4x²

Explanation:

Answer 2

{12}

Explanation:

isolate the radical expression

`√(3x) = x-6`

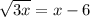
raise both sides to the index of the radical in this case 2

`(√(3x) )^(2) = (x-6)^2`

`3x = (x-6)^2`

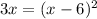
foil the right hand side or multiply (x-6)(x-6)

`3x = x^(2) -6x-6x+36`

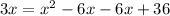
subtract 3x from both sides and combine like terms

`0=x^(2) -15x+36`

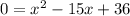
factor

`0=(x-12)(x-3)`

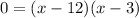
set each factor equal to zero and solve for x

x - 12 = 0 and x - 3 = 0

x = 12 and x = 3

Check each answer by plugging them individually into the original equation if the come out true they are a solution.

Check :

`√(3(12))+10=12+4\\√(36)+10 = 8\\6+10 = 16\\16=16`
`√(3(3))+10=3+4\\√(9)+10=7\\3+10=7\\13\\eq 7`

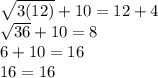
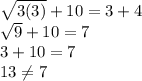
So the only solution is 12.