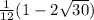Answer:
cos(a + b) =
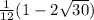
Explanation:
cos(a + b) = cos(a).cos(b) - sin(a).sin(b) [Identity]
cos(a) =
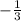
cos(b) =
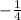
Since, terminal side of angle 'a' lies in quadrant 3, sine of angle 'a' will be negative.
sin(a) =
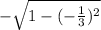 [Since, sin(a) =
[Since, sin(a) =
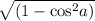 ]
]
=
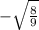
=
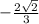
Similarly, terminal side of angle 'b' lies in quadrant 2, sine of angle 'b' will be negative.
sin(b) =
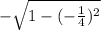
=
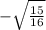
=
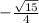
By substituting these values in the identity,
cos(a + b) =
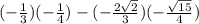
=
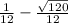
=
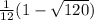
=
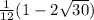
Therefore, cos(a + b) =