Question

14. Given that 16x⁴+ - 4x³– 4b²x² + 7bx + 18 is divisible by 2x + b,

(a) show that b³ - 7b² + 36 = 0,
(b) find the possible values of b.​

Answer 1

(a) check the explanation

(b) the possible values of b is 6i or -29

Step-by-step explanation:

Given function;

16x⁴ - 4x³– 4b²x² + 7bx + 18

(a)

factor of the given function = 2x + b

then, 2x + b = 0

x = -b/2

substitute the value of b into the given function;

16x⁴ - 4x³– 4b²x² + 7bx + 18

`16((-b)/(2) )^4 -4((-b)/(2))^3-4b^2((-b)/(2))^2 +7b((-b)/(2))+18=0\\\\b^4+(b^3)/(2) -b^4-(7b^2)/(2) +18=0\\\\(b^3)/(2) -(7b^2)/(2) +18=0\\\\multiply\ through \ by \`

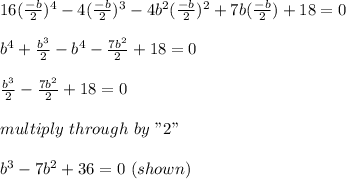
(b)

b³ - 7b² + 36 = 0

b²(b - 7) + 36 = 0

b²(b - 7) = -36

b² = -36 or b - 7 = -36

b = √(-36) or b = -36 + 7

b = √(-1) x √(36) or b = -29

b = 6i or -29