Question

An airline has two flights each day from City A to City B. A random sample of 10 morning flights left the gate an average of 15 minutes late with a standard deviation of 5 minutes. A random sample of 10 evening flights left the gate an average of 20 minutes late with a standard deviation of 3 minutes. Suppose both the morning and evening flights are 30 minutes late. To determine which flight is more late than usual, first find the z-scores. Round to one decimal place if necessary.

Answer 1

Explanation:

Let X denote the random variable that obeys the normal distribution.

Given that:

For morning flights

Mean
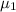`\mu_1` = 15

standard deviation
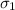`\sigma_1` = 5

Sample size
`n_1` = 10

`X_1 \sim Normal ( \mu_1, \sigma _1)`

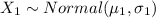
The Z - score is calculated as:

`Z = (x_1 - \mu_1)/(\sigma_1)`

`Z = (30 -15)/(5)`

`Z = (15)/(5)`

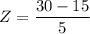
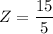
Z = 3

For evening flights

Mean
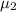`\mu_2` = 20

standard deviation
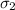`\sigma_2` = 3

Sample size
`n_2` = 10

`X_2 \sim Normal ( \mu_2, \sigma _2)`

`Z = (x_2 - \mu_2)/(\sigma_2)`

`Z = (30 -20)/(3)`

`Z = (10)/(3)`

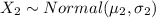
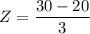
Z = 3.33

Hence, from the above z-scores, we will realize that the evening flight is more late than usual.