Question

A communications tower is supported by two wires, connected at the same point on the ground. One is attached to the tower at D and the long-on at C. The angle AD makes with the ground is 30 ° and the angle between the two wires is 10 °. How much below the top of the tower is the shorter one attached?

Answer 1

10.99 m

Explanation:

✍️What we are basically asked to solve here is to find the distance between C and D.

To find CD, find the length of BC, and BD. Their difference will give us CD.

Thus, BC - BD = CD.

✍️Finding BC using trigonometric ratio formula:

`\theta = 30 + 10 = 40`

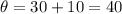
Opposite side = BC = ??

Adjacent side = 42 m

Thus:

`tan(\theta) = (opposite)/(adjacent)`

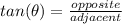
Plug in the values

`tan(40) = (BC)/(42)`

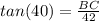
Multiply both sides by 42

`tan(40) * 42 = (BC)/(42) * 42`

`35.24 = BC`

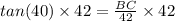
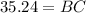
BC = 35.24 m

✍️Finding BD using trigonometric ratio formula:

`\theta = 30`

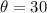
Opposite side = BD = ??

Adjacent side = 42 m

Thus:

`tan(\theta) = (opposite)/(adjacent)`

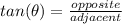
Plug in the values

`tan(30) = (BD)/(42)`

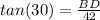
Multiply both sides by 42

`tan(30) * 42 = (BD)/(42) * 42`

`24.25 = BD`

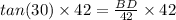
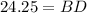
BD = 24.25 m

✍️How much below the top of the tower is the shorter one attached:

Thus,

BC - BD = CD

35.24 m - 24.25 m = 10.99 m