Answer:

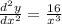
Stationary Points: See below.
General Formulas and Concepts:
Pre-Algebra
Calculus
Derivative Notation dy/dx
Derivative of a Constant equals 0.
Stationary Points are where the derivative is equal to 0.
- 1st Derivative Test - Tells us if the function f(x) has relative max or mins. Critical Numbers occur when f'(x) = 0 or f'(x) = undef
- 2nd Derivative Test - Tells us the function f(x)'s concavity behavior. Possible Points of Inflection/Points of Inflection occur when f"(x) = 0 or f"(x) = undef
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Quotient Rule:
![(d)/(dx) [(f(x))/(g(x)) ]=(g(x)f'(x)-g'(x)f(x))/(g^2(x))](https://img.qammunity.org/2021/formulas/mathematics/college/it8u9heerf1b4gbeitcwifl1w9ck0iqkzk.png)
Explanation:
Step 1: Define
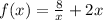
Step 2: Find 1st Derivative (dy/dx)
- Quotient Rule [Basic Power]:
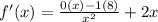
- Simplify:
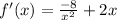
- Basic Power Rule:
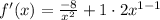
- Simplify:
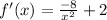
Step 3: 1st Derivative Test
- Set 1st Derivative equal to 0:
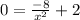
- Subtract 2 on both sides:
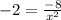
- Multiply x² on both sides:
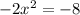
- Divide -2 on both sides:

- Square root both sides:

Our Critical Points (stationary points for rel max/min) are -2 and 2.
Step 4: Find 2nd Derivative (d²y/dx²)
- Define:
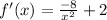
- Quotient Rule [Basic Power]:
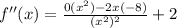
- Simplify:
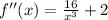
- Basic Power Rule:
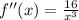
Step 5: 2nd Derivative Test
- Set 2nd Derivative equal to 0:

- Solve for x:
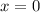
Our Possible Point of Inflection (stationary points for concavity) is 0.
Step 6: Find coordinates
Plug in the C.N and P.P.I into f(x) to find coordinate points.
x = -2
- Substitute:
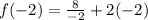
- Divide/Multiply:
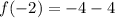
- Subtract:
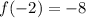
x = 2
- Substitute:
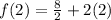
- Divide/Multiply:
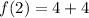
- Add:
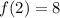
x = 0
- Substitute:
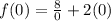
- Evaluate:
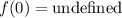
Step 7: Identify Behavior
See Attachment.
Point (-2, -8) is a relative max because f'(x) changes signs from + to -.
Point (2, 8) is a relative min because f'(x) changes signs from - to +.
When x = 0, there is a concavity change because f"(x) changes signs from - to +.