Question

2) Compare the following functions to determine which has the greater rate of change. Function 1: y = 2x + 6 Function 2: 0 4 -2 2 Y ] == a​

Answer 1

You did not clearly mention the second function. So, I am assuming you meant to say that the second function has the table values such as:

x y

0 4

-2 2

So, I am solving the question based on this information table of the 2nd function, which anyways will clear your concept.

Answer:

We conclude that the rate of change of a function '1' is greater than the rate of change of function '2'.

Explanation:

Given the function 1

`y = 2x + 6`

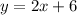
Comparing the function with the slope-intercept form of the line equation of a linear function

• 
  `y=mx+b`

where m is the rate of change or slope of the line

so

`y = 2x + 6`

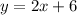
rate of change = m = 2

Now, given the function 2

x y

0 4

-2 2

Taking the slope of the two points in the table

(0 4), (-2, 2)

`\mathrm{Slope\:between\:two\:points}:\quad \mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(0,\:4\right),\:\left(x_2,\:y_2\right)=\left(-2,\:2\right)`

`m=(2-4)/(-2-0)`

`m=1`

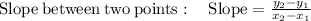
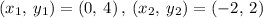
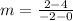
So, the rate of change or slope of the function 2 is: m = 1

Hence, we observe that:

• Rate of change of function 1 = m = 2

• Rate of change of function 2 = m = 1

As the rate of change of a function '1' is greater than the rate of change of function 2.

i.e.

m = 2 > m = 1

Therefore, we conclude that the rate of change of a function '1' is greater than the rate of change of function '2'.