Answer:
The standard deviation is considered a measure of spread.
Explanation:
Standard deviation is basically considered a measure of spread, measuring how far data values are from their mean.
- Standard deviation helps in determining the nature of the variation of the data about the mean.
For instance, in certain data sets, we may observe the same mean, but their range could be different, and data values in one data set may have been closely concentrated near the mean than the other data set values.
For example,
considering the data set
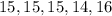
The given data set has a mean: 15
considering the second data set
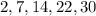
The given data set has also a mean: 15
But, the values in the second data set are clearly more spread out. When the values of a data set are not spread out largely, then the set will have a low standard deviation.
Therefore, the standard deviation is considered a measure of spread.