Question

Equations and Graphs of Rational Functions Precalculus 12

A car can travel 450 km in the same time it takes a train to travel 350 km. The car's average speed is 20 km/h faster than the average speed of the train. What is the average speed of the car? Give your answer to two decimal places.

I would just like help with figuring out the right equation for this word problem, because I cannot figure this out.

Answer 1

The average speed of the car is 90 km/h

Explanation:

The rule of the distance id D = v × t, where

• v is the speed

• t is the time

∵ A car can travel 450 km in the same time it takes a train to travel

350 km

→ That means the time of them are equals

∴ Time of the car = Time of the train

→ From the rule above t =
`(D)/(v)`

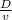
∵ D(car) = 450 km and D(train) = 350 km

∵ The car's average speed is 20 km/h faster than the average speed

of the train

→ Assume that the average speed of the train is x km/h

∴ v(train) = x km/h and v(car) = (x + 20) km/h

→ Use the rule of the time above to find the time of each one

∵ t(car) =
`(450)/((x+20))`

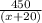
∵ t(train) =
`(350)/(x)`

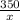
∵ t(car) = t(train)

∴
`(450)/((x+20))` =
`(350)/(x)`

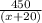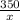
→ By using cross multiplication

∵ 450 × x = 350 × (x + 20)

∴ 450x = 350(x) + 350(20)

∴ 450x = 350x + 7000

→ Subtract 350x from both sides

∴ 100x = 7000

→ Divide both sides by 100 to find x

∴ x = 70

∵ x represents the average speed of the train

∴ The average speed of the train = 70 km/h

∵ The average speed of the car = x + 20

∴ The average speed of the car = 70 + 20

∴ The average speed of the car = 90 km/h